算法：回溯

四月的第二周，开始学习算法题：回溯算法。

在二月底就零星地看了一些算法题，当时想着从四月份开始突击一个月的算法，但因为看 Java 并发耽误了一周。从本周开始，博文内容将全部是算法。

---

回溯（backtracking）是暴力搜索法中的一种，它采用试错的思想，尝试分布地解决一个问题，在分步解决问题的过程中，当它通过尝试，发现现有的分步答案不能得到有效的正确解答时，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。

回溯是基于深度优先遍历（DFS）的一种暴力搜索方法，因此使用回溯算法的前提是，问题本身的数据结构是树，在树的基础上采取 DFS 的方式遍历，在遍历的过程中，保存符合题目条件的叶子节点。

举一个例子，比如全排列问题（给定几个数字，返回所有可能的全排列），这个问题本身就是一棵树，以[1, 2, 3]这三个数字为例，可以画成如下的树。这一类的问题我们可以通过回溯算法解决。

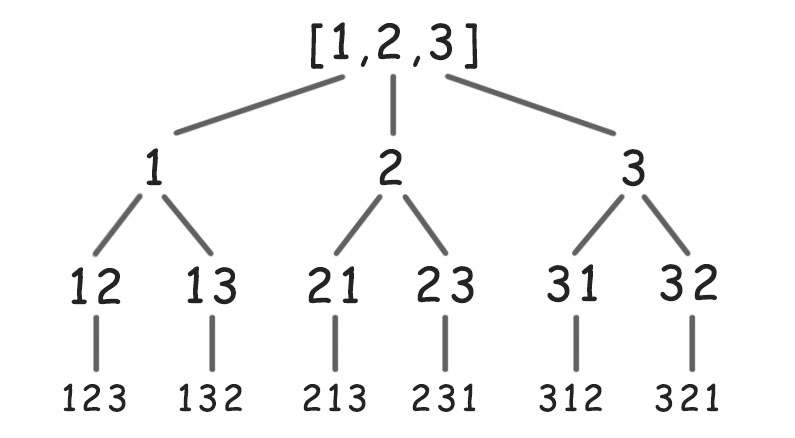
回溯算法的内核是遍历，如果一个问题能够转化为树，就可以通过回溯算法，遍历树的每一片叶子，暴力解决。在这一背景之下，回溯算法还有以下特征：

1. 遍历树的方式是递归，因此回溯是通过递归解决的。
2. 遍历树时，收集叶子（收集结果）往往有约束，比如要求结果不能重复（[1, 2]和[2, 1]只保留其中一个），收集时要根据要求收集。
3. 遍历树时，在知道某些分支下一定不可能出现结果，就可以忽略遍历这部分，这被称为“剪枝”，是回溯算法提高性能的主要方式。

下面试着整理一下套路，但是就我个人经验而言，背过了套路也用处不大，多做一点题目就会慢慢熟悉起来。推荐的做题路线是（使用 LeetCode），39 题 -> 46 题 -> 77 题 -> 78 题 -> 40 题 -> 47 题 -> 90 题，都比较简单，是用来培养手感的。

先铭记最重要的一条，做回溯算法题，第一步，先画树，画完了再做题。

回溯算法的主要流程是：试探 - 子递归 - 回溯。

doSub(list, ...){
    // ...
    list.add(item);               // 试探着加入一个元素
    doSub(list, ...);             // 子递归
    list.remove(list.size() - 1); // 把刚才试探加入的元素删掉
    //...
}

也就是先加入一个元素，执行子递归操作，再删除掉刚才加的元素。这个套路我们一会在真题中使用。

初学时由于递归使用得少，因此对递归的结构、递归的方法参数，通常会苦恼很久。在初始阶段，可以试着这么写递归：

// 最终的结果可以记在全局变量中，不设置返回值
private void doSub(List candidates, int level, Object tem) {
                           成员         递归层数    本级递归的结果
                               
    if (终止条件) {
        return;
    } else if (成功条件，准备记录结果) {
        // 记录结果
    } else {
        // ...
        doSub(candidates, level + 1, tem);
        // ...
    }
    
}

通常递归需要三个参数：操作的所有元素、递归的层数（通常用于判断什么时候要终止递归）、本级递归的结果（成功后，将参数记录下来）。这么写可能会有冗余代码（ if 的判断条件），但是按照这种思路来写，通常能写出来递归的骨架，然后再慢慢调整。

除了这三个参数之外，通常递归还需要其他参数，这个需要具体分析。就我做题而言，一般是需要增加两种参数，一会做题时详述。

LeetCode39 组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。

示例输入	示例输出
candidates = [2,3,6,7], target = 7	[   [7],   [2,2,3] ]
candidates = [2,3,5], target = 8	[   [2,2,2,2],   [2,3,3],   [3,5] ]

先画树（其实只需要画出终止条件和满足条件就足够分析了）：

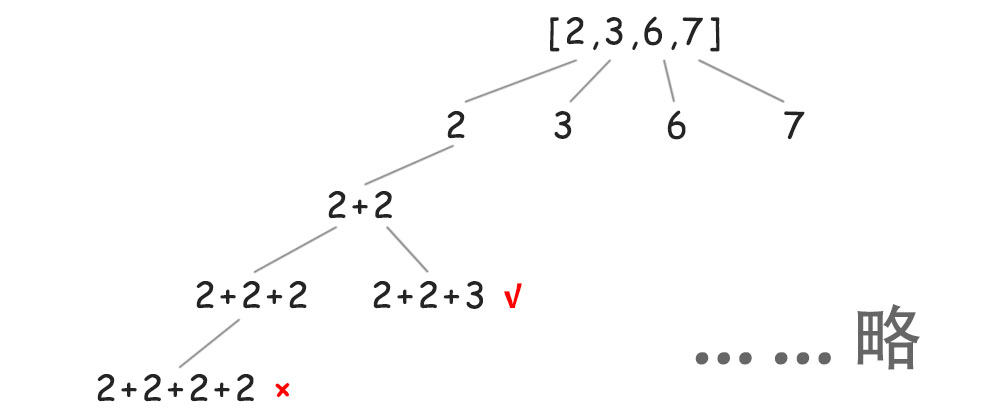
主要的逻辑是递归树

• 如果求和不足，那么继续递归
• 如果求和正好，那么记录结果，返回（返回后删除，进行下一次循环）
• 如果求和超了，那么返回（返回后删除，进行下一次循环）

public class LeetCode39 {

    // combinationSum方法返回的是什么，就直接在此定义一个该类型的变量，作为全局变量，最后直接返回该变量就可以了
    private static List<List<Integer>> result = new ArrayList<>();

    public static List<List<Integer>> combinationSum(int[] candidates, int target) {
        // 很多算法题的测试数据都会搞些数据恶心人，比如输入参数为空字符串，要预过滤
        if (null == candidates || candidates.length == 0 || target < 0) {
            return null;
        }
        // 核心逻辑，本方法是一个无返回值的方法，因为结果记录在一个全局变量result里，省去了处理返回
        process(candidates, target, new ArrayList<>());
        // 返回结果
        return result;
    }

    // 解释一下核心逻辑，每进入下一层树，在list中增加一个数字，再进入下一层递归
    // 直到求和相同时，记录求和内容
    private static void process(int[] candidates, int target, List<Integer> list) {
        // 第一步：先处理递归终止条件，此题是判断
        if (target < 0) {
            return;
        // 第二步：当递归抵达成功时，记录结果
        } else if (target == 0) {
            // 注意深拷贝
            result.add(new ArrayList<>(list));
        // 第三步：当递归没终止、没成功，准备进入下一层递归
        } else {
            // 遍历所有节点
            for (int i = 0; i < candidates.length; i++) {
                // 先加
                list.add(candidates[i]);
                // 递归
                process(candidates, target - candidates[i], list);
                // 再删，删完出循环，准备再进循环加下一个
                list.remove(list.size() - 1);
            }
        }
    }

}

上面的代码就是基础套路：

1. 定义一个全局变量记录结果

2. 递归处理

   1. 先处理递归终止，直接返回

   2. 再处理递归成功，记录结果后返回

   3. 没终止、没成功，就意味着还需要继续递归

      在循环中执行回溯算法的核心

      1. 先加
      2. 递归
      3. 再删

执行上述方法，得到这样的结果：

LeetCode39.combinationSum(new int[]{2, 3, 6, 7}, 7);
// 结果 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]]

会发现结果没有去重，出现了[2, 2, 3]和[2, 3, 2]这样内容一样但是排序不一样的情况，我们来分析一下如何去重。

重复的主要原因在于，当我们记录完[2, 2, ?]之后，进入[2, 3, ?]，选择第三个数时，我们不应当再考虑 2 了，因为在[2, 2, ?]的情况下，我们已经全部处理完有 2 的情况了，再之后我们不应该处理 2 了。细琢磨一下这句话：遍历时我们要设置一个起始点，处理过的要素，之后就跳过不参与考虑了。

这是递归新增参数的第一种情况，增加一个 int start 的参数，目的是为了在遍历时，从 start 位置开始，跳过某些元素。

private void process(int[] candidates, int target, List<Integer> list, int start) {
	// ... 
    // 每次遍历从start开始
    for (int i = start; i < candidates.length; i++) {
        // ...
    }
}

LeetCode46 全排列

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例输入	示例输出
[1,2,3]	[   [1,2,3],   [1,3,2],   [2,1,3],   [2,3,1],   [3,1,2],   [3,2,1] ]

同样，还是先画递归树：

直接写代码了噢，是完全一样的套路：

public class LeetCode46 {

    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> permute(int[] nums) {
        if (null == nums || nums.length == 0) {
            return res;
        }

        boolean[] select = new boolean[nums.length];
        doPermute(nums, 0, new ArrayList<>(), select);

        return res;
    }

    private void doPermute(int[] nums, int level, List<Integer> list, boolean[] select) {
        if (level > nums.length) {
            return;
        } else if (level == nums.length) {
            res.add(new ArrayList<>(list));
        } else {
            for (int i = 0; i < nums.length; i++) {
                if (select[i]) {
                    continue;
                } else {
                    list.add(nums[i]);
                    select[i] = true;
                    doPermute(nums, level + 1, list, select);
                    list.remove(list.size() - 1);
                    select[i] = false;
                }
            }
        }
    }
}

这里递归在原先的三个参数基础上，又增加了一个新的参数，boolean[] select，一个布尔值的数组。

对于某些题目，就比如这道题，每个元素并不是可以无限使用的，而是只能只用一次，如果使用完一次，怎么标记下来呢，就是使用一个布尔值的数组，记录下标为x的元素，已经被使用过了，不能再使用。

回溯套路，就从原来的三行，变成了五行：

list.add(nums[i]);                   ->   list.add(nums[i]);
                                     ->   select[i] = true;
doPermute(nums, level + 1, list);    ->   doPermute(nums, level + 1, list, select);
                                     ->   select[i] = false;
list.remove(list.size() - 1);        ->   list.remove(list.size() - 1);

（上一道题每个元素可以无限制地使用，因此不需要一个布尔值数组记录是否能使用）

上面的套路，只是初期不熟悉时的套路，并不能解决所有回溯问题，但是可以在初接触回溯问题时尝试做出来。最好的学习方式仍然是做题，做十几道题，就自然明白了。再发一遍学习路线（LeetCode）：39 题 -> 46 题 -> 77 题 -> 78 题 -> 40 题 -> 47 题 -> 90 题。