HashMap 与 TreeMap
十二月的第三周,来补习 Java 基础,学习 HashMap 与 TreeMap 的原理。
上周看 HashMap 的迭代器源码看上头了,觉得真巧妙哈哈,顺便还看了一点 TreeMap 的源码(但是没写),也觉得挺精妙的。那么这周来学习这两种 map 的实现。
本次所看的 Java 源码均来自于 JDK 1.8,无视之前版本的实现。
由于 HashMap 的实现需要红黑树的基础支持,因此我们先看 TreeMap,一个基于红黑树实现的 map。
TreeMap
TreeMap:形式为 tree 的 map,确切地讲,这里的 tree 是 red black tree(红黑树)。
TreeMap 实现了 SortedMap 接口,因此是一个有排序的 map,表内每个元素在存储时都是按照规则排序的。
我们在使用 TreeMap 时,不论使用哪个方法,在内部基本都会使用到 TreeMap 的基本元素 Entry 类。Entry 本身的含义指键值对(key-value),这里是一个 TreeMap 自己定义和实现的类。从结构上看,TreeMap 对象就是由一个个的 Entry 对象所组成的。因此 TreeMap 在使用方法 get()、put()、remove()……时,实际上都是在操作它自己的一个个元素 Entry。
这里以 TreeMap 的 get() 方法为例:
1 | public V get(Object key) { |
这个方法就是在调用 getEntry() 方法,根据 key 值获取一个基本存储元素:Entry。
TreeMap 的各个方法都在使用内部类 Entry,TreeMap 本身也就是由一个个的 Entry 对象组成的,因此我们先看看这个类的内部是什么样子。
Entry
1 | static final class Entry<K,V> implements Map.Entry<K,V> { |
TreeMap 内部自定义了 Entry 类,这个类实现了 Map.Entry 接口,也就是说,它是一个键值对(key-value)。
我们这里只需关注它的内部变量,其他的没必要关心(其他的是构造方法,get、set 方法,以及重写的 equals()、hashCode()、toString() 方法)。
Entry 类一共有六个成员变量:
- key 键
- value 值
- left 左节点
- right 右节点
- parent 父节点
- color 颜色
Entry 类除了 key 和 value 这两个所有 map 都必需的变量之外,还有四个成员变量,分别是左、右、父节点,以及一个布尔值变量:颜色。
成员变量里面有三个节点变量,以此能够猜出,这个类是一个节点类,比如链表里面的节点、树里面的节点等等,它能够从本节点找到其他的节点。而且变量里有左、右、父三个节点,看着就很像是二叉树的结构。
此外它还有一个布尔值变量:颜色。这个变量初见不是很理解,它有两种值,分别是红色(RED false)和黑色(BLACK true),默认是黑色的。这个布尔值变量,使得 Entry 类不光是二叉树的节点类,还是二叉树中红黑树的节点类,它在树节点之外还保留了另一种信息:类型。
红黑树
写到这里必须要开始学习红黑树了。
我把基础设定为二叉树,二叉树及之前的内容不写了。我认为二叉树作为一种数据结构,它本身是没有功能的,只能算是有实现某些功能的潜质,比如有查找速度快的潜质。为了让二叉树能够真的查找速度变快,能快速地找到存储节点,需要给二叉树增加一些规则,比如存储时要按照某种顺序,分支的深度要有限制等等。
红黑树就是一种具有一些规则的二叉树,由于这些规则的限制,使得这种数据结构在查找存储内容时会快速很多。与红黑树作用类似的还有两种(我觉得看这两种也就够了叭),一种是二叉查找树(BST, Binary Search Tree),一种是平衡二叉树/ AVL 树(G. M. Adelson-Velsky 和 E. M. Landis 发明的平衡二叉树)。当面试问到红黑树时,经常会被问到,既然有另外两种能够提高查询速度的二叉树了,为什么还需要红黑树(言下之意是问红黑树对比另外两种二叉树有什么不同),尤其是问红黑树相比于二叉查找树的优势。那么我从二叉查找树和 AVL 树开始写起,然后引到红黑树。
(这一部分基本上参考这篇文章:《记一次腾讯面试:有了二叉查找树、平衡树(AVL)为啥还需要红黑树?》)
(以及所有的图片都来源于维基百科, 本周懒得画图hhh)
二叉查找树给二叉树增加的规则是,左边比中间小,中间比右边小(左子树的节点值 < 父节点值 < 右子树的节点值),在存储的时候按照顺序存,找的时候就能很快地找到(因为有顺序了,不是漫无目的地找了)。
正常情况下,它是按照类似于二分查找法的思路去查询的。但是二叉查找树的规则约束性很有限,实际上即使按照规则,值依据链表的形式去存储也是合规的,但这样查询速度就又会慢了下来。
平衡二叉树在定义上有些模糊,我暂时认为,在通常情况下,平衡二叉树是二叉查找树的一种,即平衡二叉树的全称是【平衡二叉查找树】。在这种定义之下,平衡二叉树在二叉搜索树的基础之上,为二叉树增加了新的规则,它不光要求二叉树按照顺序存储,还要求二叉树要存储地更均衡一些,不能出现左子树一堆节点而右子树为空的情况(也就是刚才所说的类链表情况)。在维基百科里,平衡二叉树的英文名是 self-balancing binary search tree,自动平衡的二叉查找树。
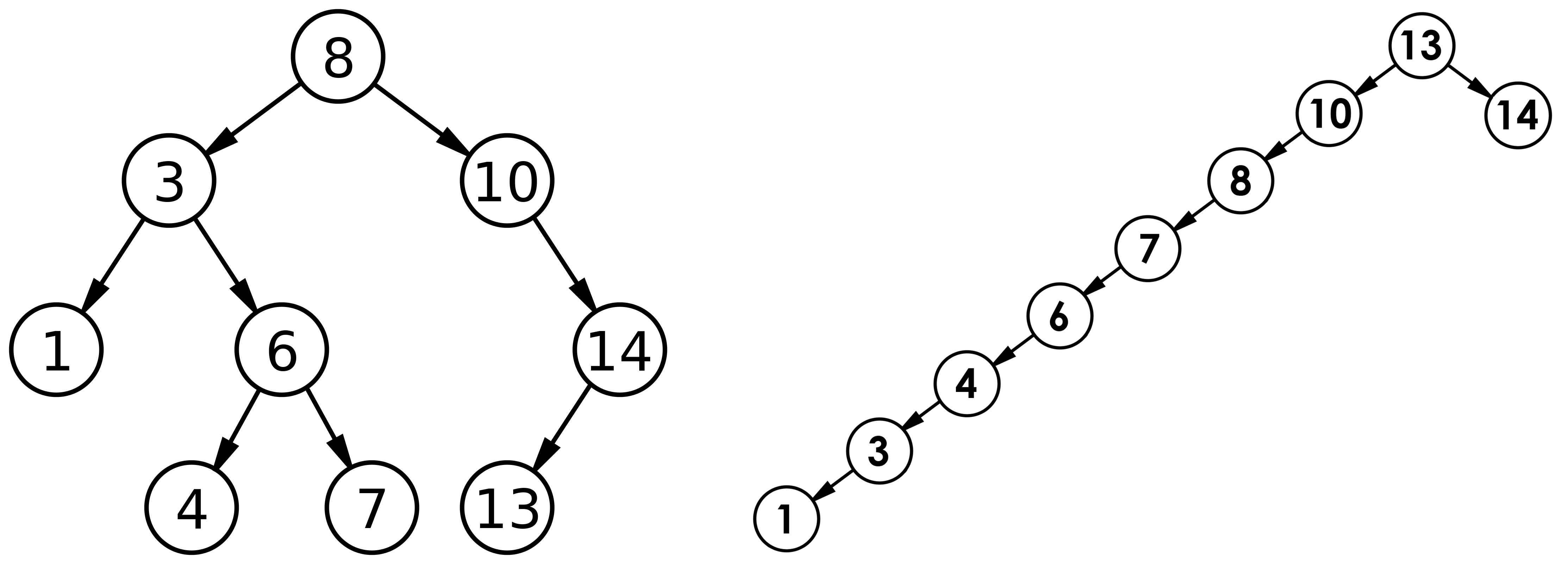
平衡二叉树有好多种,最常被 cue 的是 AVL 树,因为它是所有平衡二叉树中最平衡的那种。AVL 树在二叉查找树的基础之上,为二叉树增加的规则是,二叉树的左右子树,最大深度的差不能超过 1。下图就是 AVL 树最不平衡的状态,存在左右子树高度差达到 1 的情况,但是你应该也会觉得:这又怎么样呢,差一点点就完美平衡了。
AVL 树是最为平衡的,排列有序的二叉树,因此它在查找节点时,查询速度是相当之快的,理论上应该是平衡二叉树中查询速度最快的。但是平衡是有代价的,存储得那么有序,找起来快,存起来、删起来也慢啊。AVL 树每次插入新的节点时,如果不平衡,是通过旋转来调整平衡的。我没兴趣去探索它具体的旋转过程,但是我大概知道结论:当插入/删除节点是,AVL 树会很频繁地旋转来调整,消耗很大。
红黑树出现的意义就在于,它是平衡二叉树,但它不需要那么平衡,差不多就行,这样查询也快,插入也快。
红黑树为二叉树制定了五条规则(在数量上令小白发指):
- 每个节点有颜色,不是红色就是黑色。
- 根节点是黑色的。
- 叶子节点也是黑色的(NIL 节点)
- 中间的节点可以是红色的,但是红色节点不能连在一起(红色节点只能跟黑色节点相连)
- (平衡的核心)从任意节点出发,到每个叶子节点,应途径数量一样的黑色节点。

边看图边思考上面的规则,主要是第四、五两条规则,会发现红黑树它的平衡之处就在于,受到这些规则约束的二叉树,深度就是差得再多,在最坏的情况下,也只会差一倍(从根到叶子的最长的可能路径不多于最短的可能路径的两倍长),这种二叉树大致上是平衡的。
红黑树插入节点时同样要通过旋转来调整,但是调整的次数比 AVL 树小了很多,它虽然比 AVL 树查得慢,但是它增改节点快,是一种不错的折中选择。
终于讲完了红黑树的引入部分。
TreeMap 的 put() 方法
我这几个周看迭代器,看容器设计,感觉认识一个容器最直接、最迅速的方法,就是去看这个容器是怎么添加元素的,list 去看 add() 方法,map 去看 put() 方法。按照这种思路,去了解 TreeMap 的容器设计,应该首先去看 TreeMap 的 put() 方法,去看 TreeMap 怎么添加新的键值对。
从整体上看,TreeMap 的 put() 方法分三部分:
- 如果是首次添加,初始化容器,并直接返回。
- 按照顺序直接插入新节点。
- 调整结构,以符合红黑树的规则。
先把全部的代码展示出来:
1 | public V put(K key, V value) { | |
代码属于清晰简单的范畴,按代码的顺序简单阅读一下这段 put() 方法。
初始化
put() 方法首先获取 TreeMap 对象的根节点,这个根节点的类型就是我们最开始时说的 Entry 类,是一个存储着键值对信息的红黑树节点。
如果发现没有根节点,就说明这个 TreeMap 对象从来没有执行过 put() 方法,没有存储任意一个键值对,那么在这种情况下,把本次 put() 方法带进来的键值对作为根节点保存起来,直接返回,不执行后续内容。
1
2
3
4
5
6
7
8
9
10
11
12public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) {
// TreeMap的key和value均不能为null,这里是在检查key是否是null
compare(key, key);
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
// 后续代码...插入节点
在拿到根节点之后,put() 方法就准备插入节点了。插入节点的这部分,并不关心红黑树的约束条件,也就是说如果插入之后不满足红黑树的条件了,也是没关系的。调整树的结构以符合红黑树的约束条件,这段逻辑在 put() 方法的最后一部分。
因此,插入节点时关注的,不在于插入前后是否都符合红黑树的要求,而在于找到插入点的位置。对于 TreeMap 而言,一切节点都是按照顺序存储的,找插入点,实际上就是在找新节点应该排在什么位置上,它应该插入到
左边的节点比它小,而右边的节点比它大的位置处,当然了,前提是有一套计算顺序的规则。根据有没有计算顺序的规则,put() 方法做了一层 if-else 的判断,如果有比较器,按比较器的来,如果没有比较器,按默认排序方式来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40// ...找到根节点
int cmp;
Entry<K,V> parent;
Comparator<? super K> cpr = comparator;
if (cpr != null) { // 有比较器,按比较器排序
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else { // 没有比较器,按默认规则排序
if (key == null)
throw new NullPointerException();
("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
// 后续代码...if-else:有 Comparator
说来又是我的知识盲区,我从来没有用过 Comparator 比较器,也是因为自己函数式编程写得少。
这里的 Comparator 对象,是 TreeMap 实例化时使用构造方法带进来的:
1
2
3public TreeMap(Comparator<? super K> comparator) {
this.comparator = comparator;
}如果有比较器,那么在插入节点时,按照二分查找法的思路执行。取父节点,计算大小关系(比较器的 compare() 方法),判断往左子树走还是往右子树走,直到再无子树。
这里的 Comparator 是自己实现的,意义就在于:自己指定了一套排序规则,让 TreeMap 中的元素按照这种规则存储。
if-else:无 Comparator
如果没有自己指定排序规则,那么 TreeMap 就会按照默认的方式进行排序。默认的排序方式是,让存储的 key-value 中的 key 提供排序规则,依照 key 的类型自带的排序规则进行排序。
具体来讲,就是 【treeMap.put(key, value)】中的 key 需要实现 Comparable 接口。再换种说法解释,TreeMap 要求必须排序,如果你不主动提供排序规则,那就让 key 提供默认的排序规则(如果 key 没有排序规则,那只好报错)。
以最常见的情况举例:key 是 String 字符串。
1
2treeMap.put("str1", 1);
treeMap.put("str2", 2);这里有一处潜在的事情,那就是 String 类是实现了 Comparable 接口的,它有默认的排序规则。去看 String 类的结构体就能够发现:
1
2
3public final class String implements java.io.Serializable, Comparable<String>, CharSequence {
// ...
}实现 Comparable 接口,就必须重写 compareTo() 方法,也就是比较大小。String 类重写的 compareTo() 方法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18public int compareTo(String anotherString) {
int len1 = value.length;
int len2 = anotherString.value.length;
int lim = Math.min(len1, len2);
char v1[] = value;
char v2[] = anotherString.value;
int k = 0;
while (k < lim) {
char c1 = v1[k];
char c2 = v2[k];
if (c1 != c2) {
return c1 - c2;
}
k++;
}
return len1 - len2;
}这段代码的逻辑大意就是,字符逐个比较先后顺序,比到最后比字符串的长度。按照这种逻辑,”str1” < “str2”(结果为 -1 小于 0)。
回看刚才向 treeMap 里 put 进两个键值对(”str1” -> 1 和 “str2” -> 2),不管怎么插入,最终 treeMap 存储这两个键值对,都会是 key 为 “str1” 的键值对在前,因为在字符串的排序当中,它居前位。此时打印出 treeMap,总是会按照如下顺序输出:
1
{str1=1, str2=2}
如果 key 的类型并没有实现 Comparable 接口,没有重写 compareTo() 方法,在存入 TreeMap 时就会报错,抛出类型转换异常(ClassCastException)。
调整树结构
这部分 TreeMap 抽出了一个单独的方法,用以调整插入新节点之后的树,调整成红黑树。
1
2
3
4
5
6
7// ...已插入新节点
fixAfterInsertion(e);
size++;
modCount++;
return null;
}这部分是红黑树调整树结构的具体算法,枯燥、易忘、烧脑,正常人遇到这里都会绕开走……我只简单地看一遍,混个面熟就好。
插入的新节点默认是红色的,然后根据父节点和 uncle 节点判断左旋右旋之类的。
哎,找了个视频看,觉得麻烦得要命,算了算了,等自己强一点再回来看叭……下面是该方法的源码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
TreeMap 的其他方法暂且就不看了,转 HashMap 去了。
HashMap
HashMap 就是跟 hash 走得特别近的 map。
TreeMap 是通过 key 按顺序找到存储位置的,HashMap 是通过 key 的 hashCode 计算算出来存储位置的。
存储结构
HashMap 通过【数组+链表+红黑树】的数据结构存储键值对,很精巧的一种设计。
// 图
大体的存储逻辑是这样的:
- 先在数组里存:计算哈希值,并根据哈希值取余,得知存在数组的第几个格子中,存入。
- 有则转链表:存数组时,如果格子里面已经有数据了,则按链表的结构存(尾插法)。
- 过长则转红黑树:存链表时,如果链表过长(超过 8 个),将链表转成红黑树,之后再插入新元素,按红黑树存储。
HashMap 的 put() 方法
跟 TreeMap 一样,我们了解 HashMap 也是通过 put() 方法。
put() 方法的源码只有三行:
1 | public V put(K key, V value) { |
HashMap 的 put() 方法调用了一个私有方法,所有的代码逻辑都装在私有方法里。
这么看肯定是看不出 HashMap 的存储逻辑,但是通过 putVal() 方法的结构体,还是能够看出些东西。
1 | final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { |
hash:key 的类哈希值
调用 hash() 方法获得,将 key 的哈希值前后 16 位进行与运算,以扩大 key 的哈希值差异。这样做能够使 hashMap 在存储数据时,存储地更平均。
1
2
3
4static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}key:键
value:值
onlyIfAbsent:key 重复时是否保留原数据。
true:保留原 value
false:使用新 value
evict:留给子类 LinkedHashMap 使用的,但无论是 true 还是 false 在 LinkedHashMap 里结果都是一样的,哎懒得看了,之后有机会再看吧。
看完结构体,来看 putVal() 的具体实现逻辑:
1 | final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { | |
HashMap 的 putVal() 方法逻辑,跟 HashMap 的存储结构是完全契合的:
- 初始化 hashMap(即第一次使用 put() 方法)
- 算出数组位置后,能插入数据就插进去
- 如果不能插进去,分三种情况分析
- key 已存在,将新的 value 替换掉旧的 value
- 数组位置内已经存了链表:链表长度超过 8 则转红黑树,没超过则尾插链表
- 数组位置内已经存了红黑树:红黑树插入数据
- hashMap 内部数据过多则扩容数组(默认下,过多的标志:size > 数组长度 × 0.75)
HashMap 里的 put() 方法里有很多可以看的地方,包括【链表转红黑树】、【数组扩容】、【hash 值和负载值等的位运算】等,大概看了几眼,时间赶就不详叙述了。
这周就看到这里吧。